EXPLORING RANDOMNESS
Doubly stochastic continuous time random walk
Since its introduction some 60 years ago, the Montroll-Weiss continuous time random walk has found numerous applications due its ease of use and ability to describe both regular and anomalous diffusion. Yet, despite its broad applicability and generality, the model cannot account for effects coming from random diffusivity fluctuations, which have been observed in the motion of asset prices and molecules. To bridge this gap, we introduced a doubly stochastic version of the model in which waiting times between jumps are replaced with a fluctuating jump rate [Phys. Rev. Research 6, L012033, 2024].

We show that this newly added layer of randomness gives rise to a rich phenomenology while keeping the model fully tractable, allowing us to explore general properties and illustrate them with examples. In particular, we show that the model provides an alternative pathway to Brownian yet non-Gaussian diffusion, which has been observed and explained via diffusing diffusivity approaches.
Sokoban percolation
Alfréd Rényi humorously remarked that a mathematician functions as a contraption designed to convert coffee into theorems. Though the precise ritual of brewing one's morning cup may vary, the essence lies in the process of extraction. This requires water to find its way through the ground coffee beans and into the cup. However, can water do so effectively? And is there always a path that will allow them to percolate from top to bottom? Percolation theory emerged as an attempt to tackle this and similar questions mathematically. It can thus be ironically described as a concerted effort to convert coffee into theorems about coffee. Observe an espresso puck before (left) and after
(right) the extraction process. It is clear that as hot, pressurized, water was pushed through the puck, it did not leave the original arrangements of coffee grains intact. Rather, water paved its way through the grains, often displacing them from their original positions. In some cases, this effect is so strong that it is visible to the naked eye (see the holes formed in the used puck on the right). `With persistence, a drop of water hollows out the stone' goes the ancient Greek proverb. Yet, our understanding of percolation builds on mathematical models that completely ignore interactions between the liquid and the medium through which it percolates.

These models assume that the carrying medium is static and that it does not change in response to the percolation process. While the ability of water to push away “obstacles” that obstruct its flow is limited, it surely has some effect
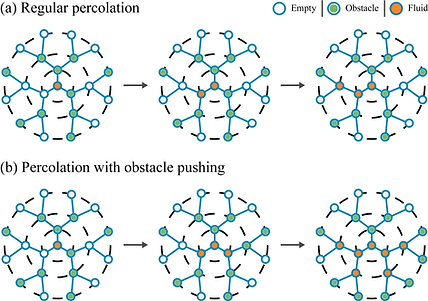
on percolation. This should be clear from the above images and discussion and is further illustrated in the figure below which compares percolation with and without obstacle pushing. Clear differences are seen between the two cases. In Panel (a), we see regular percolation where the obstacles (green) are pinned and cannot move. In Panel (b), we see percolation with obstacle pushing. This model, dubbed Sokoban percolation, was introduced by us to capture the prevalent scenario where obstacles can be pushed by the force of a fluid, or a roaming tracer [Phys. Rev. Research 5, L042015, 2023; Phys. Rev. Research 6, 023255, 2024]. Illustrated here is a case where the flow is only strong enough to push single obstacles, but this detail is non-essential and can be easily generalized.
While much is known about regular percolation, almost nothing is known about percolation with obstacle pushing. To make progress on this front, we identified a topology where this problem becomes exactly solvable [J. Phys. A: Math. Theor. 57, 33LT01, 2024]. Specifically, we turned to the Bethe lattice—a classic model in percolation theory---and randomly scattered obstacles across its nodes. We then asked: what is the probability that a fluid percolates through this lattice, i.e., establishes a continuous path from the central node to infinity? We derived an exact solution to this problem, expressing the percolation probability as a function of the initial obstacle density.
As in regular percolation, we found that this probability undergoes a second-order phase transition. We precisely determined the critical obstacle density at which this transition occurs and showed that it is higher than in the case of regular percolation. This confirms the intuitive notion that pushing facilitates percolation on the Bethe lattice. Yet this is not universally true: on a 2D square lattice, we found that obstacle pushing leads to jamming and the loss of the percolation transition [Phys. Rev. Research 5, L042015, 2023]. The stark contrast between these two topologies highlights the profound influence of network structure and underscores the need for a deeper understanding of percolation in systems where tracers interact with their environment.
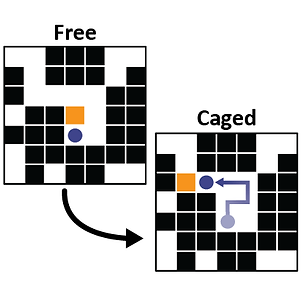
Environmental memory facilitates search with home returns
Search processes in the natural world are often punctuated by home returns that reset the position of foraging animals, birds, and insects. Many theoretical, numerical, and experimental studies have now demonstrated that this strategy can drastically facilitate search, which could explain its prevalence. To further facilitate search, foragers also work as a group: modifying their surroundings in highly sophisticated ways, e.g., by leaving chemical scent trails that
imprint the memory of previous excursions. We collaborated with the group of Yael Roichman to show that the benefit coming from such environmental memory is significant even for a single, nonintelligent searcher that is limited to simple physical interactions with its surroundings [Phys. Rev. Research 6, 023255, 2024]. To this end, we employed a self-propelled bristle robot that moves randomly within an arena filled with obstacles that the robot can push around. To mimic home returns, we reset the bristle robot's position at constant time intervals. We showed that trails created by the robot gave rise to a form of environmental memory that facilitated search by increasing the effective diffusion coefficient. Numerical simulations and theoretical estimates designed to capture the essential physics of the experiment supported our conclusions, indicating that these are not limited to the to the particular system studied in the experiment.

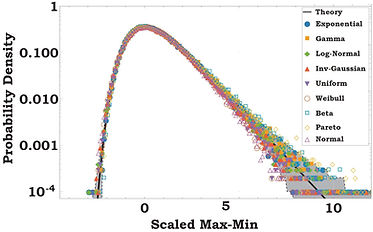
Universal statistics for Min-Max/Max-Min of large random matrices
The Max-Min and Min-Max of matrices arise prevalently in science and engineering. However, in many real-world situations, the computation of the Max-Min and Min-Max is challenging as matrices are large and full information about their entries is lacking. In this duo of papers [Phys. Rev. E 100, 020104(R), 2019; Phys. Rev. E 100, 022129, 2019], we took a statistical-physics approach and established limit laws—akin to the central limit theorem—for the Max-Min and Min-Max of large random matrices. The limit laws assert that Gumbel statistics emerge irrespective of the matrix entries' distribution. The universality and simplicity of this result makes us hopeful that it will find various applications.
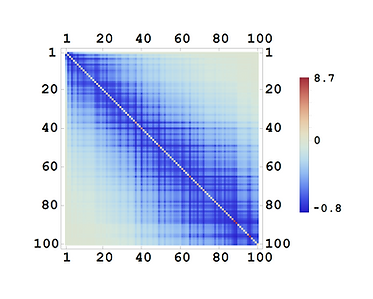
Occupancy correlations in the asymmetric simple inclusion process
The asymmetric simple inclusion process (ASIP) is a lattice-gas model for unidirectional transport with irreversible aggregation [Phys. Rev. Lett. 109, 020603, 2012; Phys. Rev. E 84, 041101, 2011]. To date, the analytical tractability of the model has been rather limited: while the average particle density is easy to compute, very little is known about the (full) joint occupancy distribution of particles. To partially bridge this gap, we studied occupancy correlations in the ASIP [Phys. Rev. E 100, 042109, 2019]. An exact formula for the covariance matrix of the occupancy vector at the steady-state was derived and corroborated against numerical simulations.